cuerpos geométricos
una figura geométrica es un conjunto no vació cuyos elementos son puntos. las figuras geométricas son el objeto de estudio de la geometría ,rama de las matemáticas que se dedica a analizar las propiedades y medidas de las figuras en el espacio o en el plano.

POLIEDROS
Un poliedro es un cuerpo geométrico cuyas caras son planas y encierran un volumen finito cuando las caras tienen las mismas superficies, reciben el nombre de poliedros regulares en este caso los ángulos diedros y poliedros tienen la misma medida.

clasificación de los poliedros:
tetraedro
un tetraedro es un poliedro de cuatro caras.
con este numero de caras ha de ser un poliedro convexo,y sus caras triangulares encontrándose en tres de ellas en cada vértice.
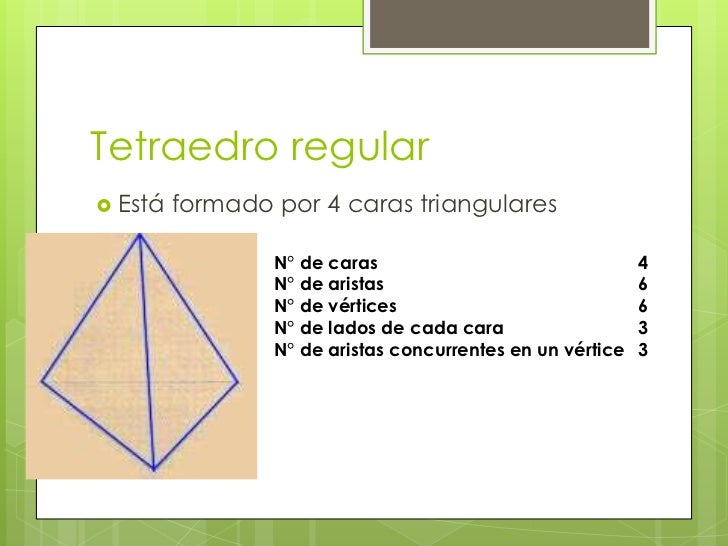
área del tetraedro:

volumen del tetraedro:

octaedro
un octaedro es un poliedro de ocho caras con este numero de caras puede ser un poliedro convexo o un poliedro cóncavo. sus caras han de ser polígonos de siete lados o menos

área del octaedro:

volumen del octaedro:

http://www.vitutor.com/geo/esp/v_2.html
icosaedro
un icosaedro es un poliedro de veinte caras, convexo o cóncavo. si las veinte caras del icosaedro son triángulos equilateros y congruentes , iguales entre si, el icosaedro es convexo y se denomina regular, siendo entonces uno de los llamados sólidos platónicos.
https://es.wikipedia.org/wiki/Icosaedro
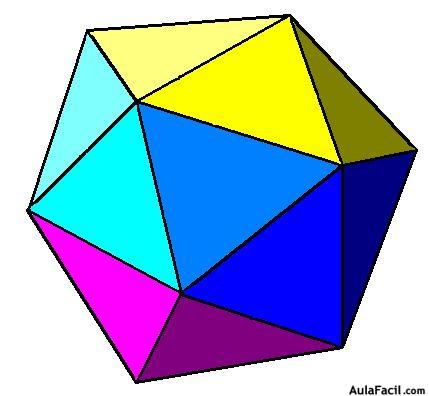
area del icosaedro:

volumen del icosaedro:

hexaedro
un hexaedro es un poliedro de seis caras.
con este numero de caras ha de ser un
poliedro convexo, y su caras han de
ser polígonos de cinco lados o menos . si las
seis caras del hexaedro son cuadrados
congruentes, el hexaedro se denomina
regular.

área del hexaedro:

volumen del hexaedro:
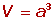
http://www.ditutor.com/geometria_espacio/hexaedro.html
dodecaedro
un icosaedro es un poliedro de doce caras,
convexo o cóncavo. sus caras han de ser
polígonos de once lados o menos. si las
doce caras del dodecaedro son pentágonos
regulares, iguales entre si, se denomina
regular.
https://es.wikipedia.org/wiki/Dodecaedro
área del dodecaedro:

volumen del dodecaedro:

http://www.vitutor.net/2/2/17.html
No hay comentarios:
Publicar un comentario